User:Chas zzz brown/polya enumeration
{{Expert|date=March 2009}}
- "Enumeration theorem" redirects here. For its labelled counterpart, see Labelled enumeration theorem.
The Pólya enumeration theorem (PET), also known as Redfield–Pólya's Theorem, is a theorem in combinatorics, generalizing Burnside's lemma about number of orbits. This theorem was first discovered and published by John Howard Redfield in 1927 but its importance was overlooked and Redfield's publication was not noticed by most of mathematical community. Independently the same result was proved in 1937 by George Pólya, who also demonstrated a number of its applications, in particular to enumeration of chemical compounds.
The PET gave rise to symbolic operators and symbolic methods in enumerative combinatorics and was generalized to the fundamental theorem of combinatorial enumeration.
Preliminaries
[edit]The weight function
[edit]A frequent technique in combinatorics is to use a generating function to count the number of objects in a set S having a desired property. If T(z) is such a generating function of the form:
then the coefficient typically counts the number of elements of S characterized by the natural n. For example, might count the number of partitions of having exactly n partitions, or the number of graphs with n vertices, or the number of 8-bit binary numbers having n "1"s, and so on. In any case, we then say that an element of S which is counted by has a weight of ; and more formally we say there is a weight function
which maps the elements of S to powers of z. This mapping is purely abstract: there is no numeric value to be associated with z which will be squared, cubed, etc. Instead the motivation is that we can then relate the generating function T and the weight function w as follows:
In some cases, a more complicated generating function over more variables is used to give a more precise ability to count diverse objects. For example, we might use a generating function of the form:
to enumerate a set S of colorings of some family of shapes, where represents any coloring having a elements of the shape colored red, b elements colored green and c elements colored blue; and where the corresponding coefficent is the number of colorings having that configuration.
We again say that a coloring to be counted has a weight of ; and that there is a weight function
which maps the colorings of the shapes to products of powers of x, y, and z; and we again have the equality:
Slots, figures, and mappings
[edit]Many combinatorial problems can be expressed as counting equivalence classes of mappings from some domain set D into some range set R; and part of the technique of applying PET is to choose D and R appropriately for the situation at hand.
A natural example of this type of mapping is a coloring of the faces of a cube where each face is either red, green or blue. We let the set F = {1,2,3,4,5,6} represent the six faces of the cube, and the set C = {red, green, blue} be the possible colors of any face. Then a particular coloring c is a function of the form:
and the set of all such mappings is the set of functions .
More abstractly, suppose we wish to characterize a graph on three vertices. We let the set be the set of possible edges in such a graph, and let P = {no, yes} represent the two possibilities "no, the edge is not present in the graph" and "yes, the edge is present in the graph". Then a particular graph G can be represented by a mapping of the form:
and the set of all such mappings is the set of functions .
In each case, we have a domain set D which can be thought of as defining a set of "slots to be filled"; and a range set R consisting "figures which can occupy a slot"; and the combinatorial objects under consideration can then be represented by a mapping of slots into figures.
Configurations as equivalence classes of mappings
[edit]Our goal is not to count all the functions from the domain set D to the range set R (this is usually a trivial task); instead, there is some symmetry in the problem which renders different mappings as corresponding to the same configuration for the purposes of our counting.
In the case of colorings of the cube, the symmetry is geometric; but in problems of counting objects such as trees, we usually want to consider the order of the children of a node as being irrelevant to whether two trees are identical.
This can be both generalized and formalized by saying that there is a group which acts on the elements of the domain set ("the slots") of our mappings. We define a relation for two mappings if there is an element such that:
Since A is a group, it follows that is an equivalence relation, and this allows us to define the equivalence class for each mapping f under the action of A.
We will then define a configuration to be an equivalence class of mappings of our domain set ("the slots to be filled") to our range set ("figures which are assigned to slots").
Associating weight functions with the figures, mappings and configurations
[edit]As noted initially, our goal is to produce a generating function T which enumerates the various configurations by weight.
In the particular case of colorings of the cube with 3 colors, we want to associate a weight of with any mapping having a red faces, b green faces, and c blue faces. To accomplish this, we first define a weighting function on the figures (range set) as follows:
and then for any coloring , we define the weight function W as:
Then a coloring such as (red, green, green, blue, red, red) has a weight of (x y y z x x) = x3 y2 z, as was desired.
In the case of graphs on three vertices using the notation above, we define the weight function on the figures as:
We again define the weight of a mapping which represents a graph G as:
Then a mapping such as (no, yes, yes) yields a weight of (1 z z) = z2; so a graph with two edges has a weight of z2, again as desired.
Furthermore, it follows that if then using the definition of W given in the previous section, .
To see this, note that since each acts bijectively on , then if we have that there exists such that:
Intuitively, permuting the order of the elements of a product does not change the value of the product. Therefore, we can safely extend the definition of the weight of a mapping to the weight of an equivalence class by way of .
The question PET answers
[edit]This allows us to state the question which the PET will ultimately answer:
Given the domain set D and the range set R, let C be the set of equivalence classes under the action of the group A on D of the set of all functions . Given the weight function w on R, define the generating function T by:
Then the coefficients in the expansion of T count the number of distinct configurations by weight. So the question is: how can we determine the coefficients in the expansion of T?
Informal Statement of the PET
[edit]Suppose we have a set X of n objects, and a set Y of labels which will be applied to each of the elements of X. We will say "c is a coloring of X" to mean that c is a function of the form .
Often there is the additional constraint: there is a group G which acts on X, where G represents some geometric symmetry which renders certain colorings of X equivalent. More formally, we consider two colorings and to be equivalent if and only if there is there is some element g of G with
If we are only interested in counting the total number of different equivalent colorings of X, then we can use Burnside's lemma. But we often want to know more specifically how many different equivalent colorings of X there are which satisfy some additional constraints. For example, we might want to count the number of different equivalent colorings of X where exactly two elements of X are assigned the color c1 from Y.
To this end, we first posit a weighting function w : Y -> R, where R is a ring such as the integers or, more commonly, a polynomial ring over the integers such as , , etc. In any case, R and w are chosen so that w encodes the particular features of Y which will be of interest.
The weighting function is then extended to map colorings into the same ring R; given a coloring c, we define w(c) = sum(w(c(x)).
Z, Z[x], Z[x,y]
Suppose you have a set of n slots and a set of objects being distributed into these slots and a generating function f(a, b, ...) of the objects by weight. Furthermore, there is a permutation group A acting on the slots that creates equivalence classes of filled slot configurations (two configurations are equivalent if one may be obtained from the other by a permutation from A). Then the generating function of the equivalence classes by weight, where the weight of a configuration is the sum of the weights of the objects in the slots, is obtained by evaluating the cycle index Z(A) of A i.e.
at
Definitions for the univariate case
[edit]We have two sets and , as well as a weight function . For reasons that will become clear, typically w is defined so that for some natural k for each .
Consider the set of all mappings . We can define the distinct weight of a function to be
- .
This implies equality of the weight W for all those functions which are equivalent under the action of the group A. Note that every subgroup of the symmetric group on elements, , acts on through permutations. If is one such subgroup, an equivalence relation on is defined as
- for some
Denote by the equivalence class of with respect to this equivalence relation. In group theoretical terms, is the orbit of under the action of A. Since each acts bijectively on , then
Intuitively, permuting the order of the elements of a product does not change the value of the product. Therefore, we can safely define .
Generating function by weight of the objects being distributed into the slots
[edit]Let
- - the number of elements of of weight ;
The generating function by weight of the source objects is
Generating function by weight of the filled slot configurations (orbits)
[edit]Let
- - the number of orbits of weight ;
The generating function of the filled slot configurations is
- .
Theorem statement
[edit]Given all the above definitions, Pólya's enumeration theorem asserts that
where is the cycle index of .
Example computations
[edit]Enumerating graphs on three and four vertices by the number of edges
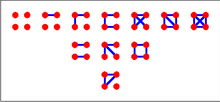
[edit]The graphs on three vertices without taking symmetries into account are shown at right. There are i.e. 8 of them ( gives the number of pairs of vertices, i.e. edges, chosen from among three vertices).

We want to enumerate these graphs taking symmetries into account. There are only four nonisomorphic graphs, also shown at right.

In this problem is the set of all edges between vertices and is . Each mapping defines a graph on the vertices. If we define , then is the number of edges in the graph resulting from . Clearly, - there are 2 elements in , one of weight 0 and one of weight 1.
The graph preserving edge permutations are directly generated by permutations of the vertices. Therefore, the subgroup of acting on the edges (the edge permutation group of the graph) is of size .
The cycle index of the permutation group of the edges is[1]
It follows from the enumeration theorem that the generating function of the non-isomorphic graphs on 3 vertices is
or
which says that there is one graph with three edges, one with two, one with one edge, and one with no edges.
The cycle index of the edge permutation group for graphs on four vertices, which has degree six (there are six edges) and order twenty-four (each vertex permutation of the four vertices induces an edge permutation) is:[2]
Hence
or
These graphs are shown at right.
A program that computes the generating function of the nonisomorphic graphs on vertices as well as a detailed description of the algorithm used can be found in the GNUstep cookbook.[3]
Enumerating rooted ternary trees
[edit]X

The set T3 of rooted ternary trees consists of rooted trees with outgoing degree <= 3. Examples of these trees on 0, 1, 2, 3, and 4 vertexes is shown as def. 1 in the figure at the right.
An alternative definition which is more amenable to enumeration is to define T3 as the set of trees having at least one vertex, and where every vertex has outgoing degree 0 (in which case we will call the vertex a leaf), or outgoing degree 3 (in which case we will call the vertex a node). Examples shown at right with 0, 1, 2, 3, and 4 nodes is shown as def. 2 in the figure. Note that there is a bijection between the objects in the two definitions by mapping vertices in the first definition to nodes in the second definition. The second definition will be used in the remainder of this section.
Two trees that can be obtained from one another by repeatedly permuting the children of some node are considered equivalent. In other words, the group that acts on the children of a node is the symmetric group S3; and the figures at right are actually representatives of the equivalence classes of trees under this action when it is applied to every node of the tree.
Using the PET, we will find a generating function T which enumerates the number of equivalence classes for ternary trees having 0, 1, 2, ... nodes.
We first note the following recursive definition of T3: an element of T3 is either a leaf, or a root node with three children which are elements of T3 where ordering of the children is ignored.
We can express "f is a root node with three children in T3" as saying that f is a function of the form:
and we want to use the PET to count only the equivalence classes of such functions so that the ordering of the children is ignored.
To apply the PET, our function's domain set is , and its range set is R = T3. Alternatively we can consider that the "slots" in this problem are the three required children of the root node of the tree, and the "objects" that go into these slots are to be taken as elements of T3 itself.
The group that acts on the domain ("slots") is the symmetric group S3 with cycle index
Define the weight of a figure in T3 as , where n is the number of nodes in the figure (the range of our weighting function w is therefore the polynomial ring ). We then have that the generating functions for both the figures and the configurations are the same:
(although at this point we only know that t0 = 1). It follows that the functional equation for the generating function T(z) of the set T3 of rooted ternary trees is
This translates into the following recurrence relation for the number tn of rooted ternary trees on n nodes:
and
where a, b and c are nonnegative integers.
The first few values of are
Enumerating necklaces with double colors
[edit]Suppose you have a necklace containing beads of different colors, where every color is present exactly twice. How many different necklaces are there where two necklaces are considered equivalent if there exists a sequence of rotations and/or reflections that transforms one into the other?
In this problem the slots are the locations where beads may be placed on the necklace and the objects that go into them are the beads. The group that acts on the slots is the dihedral group The three types of symmetries that may occur are illustrated at right for the case

They are: rotations, reflections in an axis passing through opposite beads and reflections in an axis passing through opposite links.
The cycle index of the dihedral group is is
where the sum represents the rotations, the second term the reflections in an axis passing through opposite beads, and the third term, the reflections in an axis passing through opposite links.
Let the variable represent the first color, the second, the third and so on, up to . The number of necklaces is then given by
Considering the rotations first, we see that only and contribute, namely through
and
The reflections in an axis passing through opposite beads contribute
or
because there are ways to choose a color from the first term, and ways to choose the remaining colors from the second term (sum of squares raised to the th power).
Finally, the reflections in an axis passing through opposite links contribute
This yields the closed form expression for the number of necklaces containing different colors exactly twice:
The first few terms are
This problem appeared on the newsgroup es.ciencia.matematicas.[4]
Enumerating colored cubes
[edit]Suppose you have an ordinary cube in three-space whose faces may take on one of three colors and are being permuted by the automorphisms of the cube (rotations in three-space). Here the slots are the six faces and the objects that go into them are the three colors. The object generating function by weight is
which indicates that there are three colors and every color has weight one.

The cycle index of the permutation group C of the faces is[5]
It follows that the generating function of the equivalence classes i.e. colored cubes taking symmetries into account is
or
This says e.g. that there is one cube using color x on five faces and color z on the sixth, and there are six cubes using x, y, and z twice:
- the cube where opposite faces have the same color
- the three cubes where two opposite faces have the same color and the remaining two pairs of opposite faces do not
- the two cubes where opposite faces always have different colors.
It also says that there are three cubes using color x on three faces, color y on two faces and color z on the remaining face:
- the cube where all faces of color x share a vertex
- the cube where the two faces of color y are adjacent to all three faces of color x
- the cube where one face of color y is adjacent to only two faces of color x.
Note that and there are 57 distinct colored cubes in total when there are three colors.
Formal statement of the theorem
[edit]The following statement of the theorem is for the general multivariate case as in the example of the colored necklaces and cubes.
Let be a group acting on a set (the "slots") and consider the set of all functions from a set to a weighted set (the objects) with weight function (the "filled slot configurations"), where the weight of a function f is the sum of the weights of its range.
The Pólya enumeration theorem states that the sum of the weights of the orbits of on (the equivalence classes of configurations induced by X) is given by
- .
When is a monomial in the variables (including constants) we have
where
is the generating function of the set Y by weight. Hence
and we obtain the alternate form
Proof of theorem
[edit]The Pólya enumeration theorem follows from Burnside's lemma, which says that the number of orbits (equivalence classes of filled slot configurations) is the average of the number of elements of fixed by the permutation g of A over all permutations g. This value is a number and yields the count of the orbits, whereas PET enumerates orbits by weight, a more detailed classification, from which the count may be recovered by setting all variables of the weight function to one.
Applying the lemma to orbits of weight , the number of orbits of this weight is
where is the set of functions of weight fixed by g.
Summing over all possible weights we have
Let the cycle structure of g be represented by
If g fixes an element of then it must be constant on every cycle q of g. The generating function by weight of a cycle q of |q| identical elements from the set of objects enumerated by f(a, b, c, ...) is
It follows that the generating function by weight of the points fixed by g is the product of the above term over all cycles of g, i.e.
or
Substituting this for in the sum over all g yields the substituted cycle index as claimed.
Notes
[edit]- ^ Cycle index of the edge permutation group of graphs on three vertices
- ^ Cycle index of the edge permutation group of graphs on four vertices
- ^ Marko Riedel Pólya's enumeration theorem and the symbolic method and The GNUstep cookbook
- ^ Discussion in es.ciencia.matematicas (in Spanish)
- ^ Cycle index of the face permutations of a cube
References
[edit]- Redfield, J. Howard (1927). "The Theory of Group-Reduced Distributions". American Journal of Mathematics. 49 (3): 433–455. doi:10.2307/2370675. MR 1506633.
- Frank Harary (1967). "The Enumeration Methods of Redfield". American Journal of Mathematics. 89 (2): 373–384. doi:10.2307/2373127. MR 0214487.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - G. Pólya (1937). "Kombinatorische Anzahlbestimmungen für Gruppen, Graphen und chemische Verbindungen". Acta Mathematica. 68 (1): 145–254. doi:10.1007/BF02546665.
- G. Pólya (1987). Combinatorial Enumeration of Groups, Graphs, and Chemical Compounds. New York: Springer-Verlag. ISBN 0-387-96413-4. MR 0884155.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help)
External links
[edit]- Applying the Pólya-Burnside Enumeration Theorem by Hector Zenil and Oleksandr Pavlyk, The Wolfram Demonstrations Project.
- Weisstein, Eric W. "Polya Enumeration Theorem". MathWorld.
- Frederic Chyzak Enumerating alcohols and other classes of chemical moleculs, an example of Polya theory.



![{\displaystyle [1,2,3...,k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6dfd7a890b7bf721c81337bfbaad86e4acea0e4c)

![{\displaystyle w:S\rightarrow \mathbb {Z} [z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7c47cbbac779350a0398cb463c3bbb81476746e)

![{\displaystyle T(x,y,z)\in \mathbb {Z} [[x,y,z]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17302afead38b128b62393d1169800de7fc373d8)



![{\displaystyle w:S\rightarrow \mathbb {Z} [x,y,z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ad808ec05904dc77d3e10cb0e3b47840fda9bed)













![{\displaystyle [f]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1dfdc5a27aa518c9a0e4369c132a1995073ee3c9)






![{\displaystyle g\in [f]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7a4ed4623cade39d8ef1698a6469c966af50f57)



![{\displaystyle W([f])=W(f)\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8e79afc510d74ade9da575384addd781a96c63a)

![{\displaystyle T=\sum _{[c]\in C}W([c])=\sum _{[c]\in C}\prod _{d\in D}w(c(d))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05479ee6b7bc798253e727d330eb682d212baba5)





![{\displaystyle \mathbf {Z} [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aac7eed710c6ea31abc079fb2a2129132a1b7969)
![{\displaystyle \mathbf {Z} [x,y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0fbdeba29b65072d2f77296c3b69127019b43e6)




![{\displaystyle w:Y\rightarrow \mathbb {Z} [t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26303897ce0015f5d265ff1c593a16736b7d8e54)









![{\displaystyle [f]=\{g\in F\mid f\sim _{A}g\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6024d35447d9e3de316c4fd6f71ca1a6668f4a7e)





![{\displaystyle C_{k}=\left|\{[f]\mid W([f])=k\}\right|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08c4c15c19ec9d88f5410dc590e83ee689d4b375)





















![{\displaystyle [f]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7414a730e8157655ff770265ec3a03ec9f09dd54)


![{\displaystyle \mathbb {Z} [z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae41c130c6d9a25638e6a448abd520169f398a5b)












![{\displaystyle [c_{1}^{2}\,c_{2}^{2}\,c_{3}^{2}\,\cdots \,c_{n}^{2}]Z(D_{2n})(c_{1},c_{2},c_{3},\ldots c_{n}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9c0fa35e1cbddb7ac1248e22b47062c2ad92c50)


^{2n}={2n \choose 2,2,\ldots 2}={\frac {(2n)!}{2^{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55cbb66d8c43a4c27938dd39d36a01897ebba9d4)
^{n}={n \choose 1,1,\ldots 1}=n!.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7a20f02fbe74ff66b6d7370cd0eab147dd3bffe)
^{2}(c_{1}^{2}+c_{2}^{2}+\cdots +c_{n}^{2})^{n-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/291500ed84da37cc46e37db3e486abefa87e5937)



^{n}=n\,{n \choose 1,1,\ldots 1}=n\,n!.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb6ef28b6e9d5ecd2c608999bd5b71aed4b11d38)

























